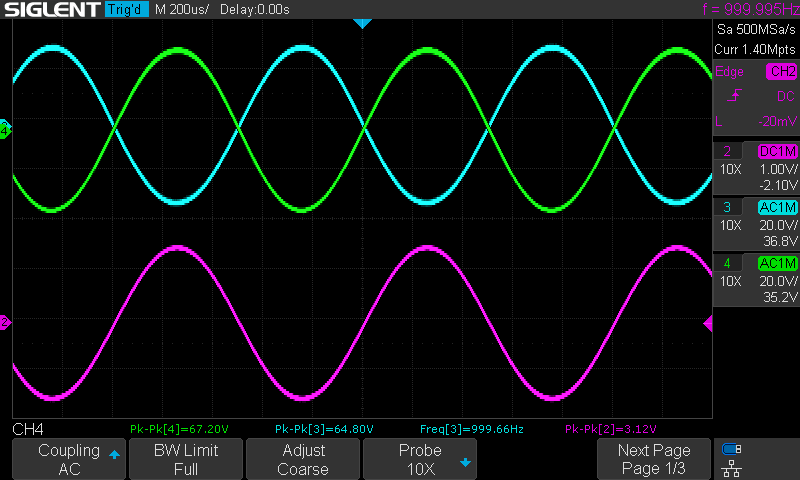
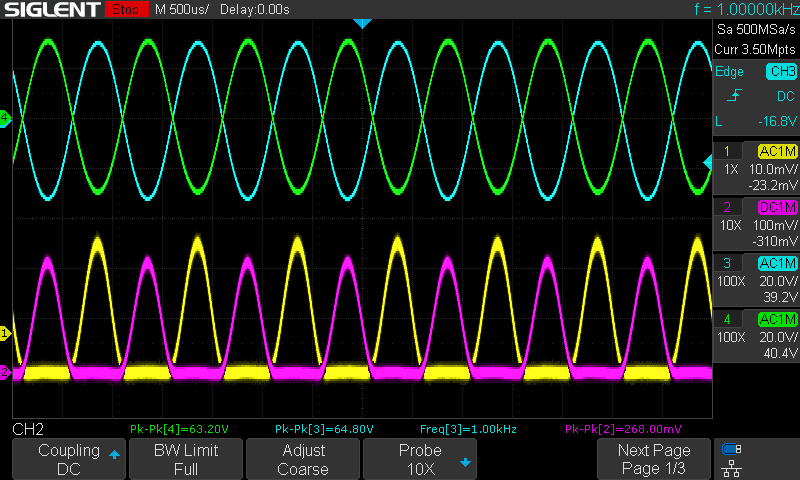
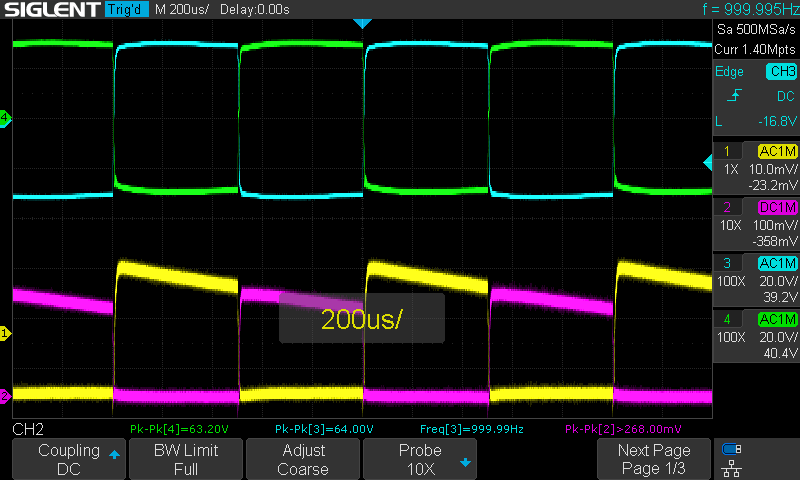
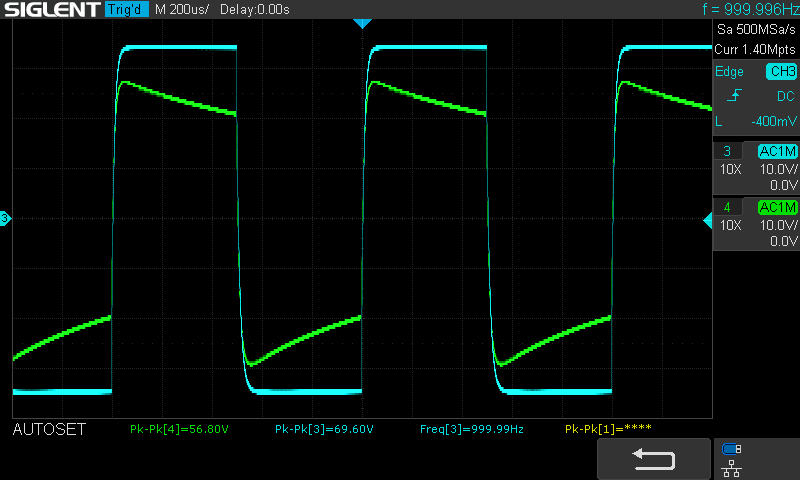
Produced from 1985-1997, the Onkyo 9090 FM tuner is the best FM tuner Onkyo ever produced (with the exception of a rare model that is very similar). The 1990s being the golden age of FM tuners. After that the mass market moved toward home theater and digital sound sources, leaving the 1990s with tuners that remain outstanding even today. It has excellent sound quality and is able to pull in weak signals better than almost any tuner of that era or today, at least for under $800. Magnum Dynalab has an excellent line of very expensive and performant FM tuners today–but I think their cheapest model is around $800.

I have purchased three of these from Ebay, and one thing they all have in common is that the large power supply capacitor next to a voltage regulator have blown out over the years. Two of the units had electrolyte from the capacitors on the circuit board, and the one I will talk about today had been sloppily repaired with an axial capacitor replacing the large cap which presumably blew sometime in the previous decades. The problem with the 9090 is a design flaw from Onkyo, where a physically large capacitor is too close to the heat sink of a voltage regulator, which roasts it.

When I get a 9090 used, they normally have spilled and baked on electrolyte from this capacitor. I am able to remove the crust by scraping it with a piece of wood and clean it with alchohol. Even in this degraded state, the tuner still works, but there is no need for me to leave it in that degraded state.

In this unit, I replaced all of the electrolytics, and ensured that the capacitors closest to the heat sink were rated for 125 degrees centigrade. I also thought about ways to increase the surface area of the heat sink, and ultimately decided to use a thermally conductive epoxy to glue two heat pipes onto it. The photo below shows the positioning of the voltage regulator heat sink and the capacitor, which runs at about 63 degrees centigrade according to my inexpensive infrared thermometer. I also note that the chassis of the 9090 has almost nothing in terms of ventilation and airflow past these hot parts.

This is what it looks like after I added the heat pipes. Again, not very scientific, but the heat sink appears to be running at 53 degrees centigrade with the heat pipes, a 10 degree improvement. 50/60 degrees does not seem very hot compared to caps rated for 85-125 degrees, but these measurements are before the top is put on the tuner and airflow will be reduced. Also, a 125 degree cap is rated for that temperature for something like 2000 to 400 hours. For electrolytics, heat is their mortal enemy, but I think the higher rated caps have a chemical paste inside that is formulated to tolerate higher temperatures longer than a typical 85 degree cap would. Presumably cap technology has also improved in the last 30 some years. When I do a re-cap, I typically select the most expensive cap that meets the electrical requirements, so I hope that improves the situation overall.

The heatpipes glued on. The dark spots are reflections in the light, not discoloration of the metal. I hope that the heatpipes are more effective than simply pieces of copper, but no way of knowing.

The view from the top–showing how close that cap is to the heat sink.

Another interesting aspect about re-capping this was a 22,000 uf capacitor that retains the presets when the unit is not plugged in. The original cap was the diameter of a dime and maybe 3/4 inch tall. I could not find a 220,000 uf cap of such small dimensions, so I got the size that was available and physically mounted it on some spare chassis space, since it is too tall to go in the PCB where the original one was. I missed this cap the first time I ordered parts because it was specified as something like .022 f. I thought it was .022 uf and would not be an electrolytic. After taking a closer look, I realized I missed the fact it was specified in farads–I have never seen that before in a schematic or parts list.

That’s about all I can say about fixing up my 9090. Its a monster in terms of physical size, it has great RF performance, and sounds great as well. Its clarity shows the overly compressed and greatly degraded sound quality in most pop and rock stations. Only our local jazz station, 88.5 and classical music station 99.5 demonstrate how wonderful FM can sound.

I love the Bryston 2B, its powerful and smooth and is only one rack unit tall. I have a pro model that I got, presumably after it was scrapped by the Canadian Broadcasting System. Its got some wear on the outside, but the electronics are in pristin condition. I replaced the electrolytic caps a couple of years ago, and when I recently re-capped a retail model 2B that I got on ebay, I replaced the stock 4700 uf power supply caps with 6800 uf ones, which due to newer technology is the same size as the original 4700 uf caps were.

The pro model is designed for use in a professional facility and does not have an on/off switch. It also comes with balanced XLR jacks in the back which are standard in the industry. Well, its kind of a hassle to hook these up to my un-balanced home stereo stuff–I was using a high fidelity balanced to unbalanced transformer.

When reading an ad for a 2B on ebay, the seller noted that he had replaced the balanced inputs on a pro with the consumer standard RCA jack. He noted that the input to the amp proper is single ended, not balanced, and the interface to the XLR jack is done with a small adapter circuit that contains an op amp, and horror of horrors to an audiophile, passes the signal through an electrolytic capacitor on its way to the amp. I studied the circuit diagrams of the pro and retail models and saw that the retail simply took the input from the RCA jack and fed it straight to the input pin on the amp module circuit board. I resolved to implement it that way.

To physically mount the RCA jack onto the XLR hole in the chassis, I found an adapter for that very purpose on ebay. They were expensive to my thinking, about $20 each, but when I received them I noted they were made from aluminum and were mechanically and electrically very sound, so to speak…

Working with the tiny shielded cable was tedious but I was able to create good solder connectios on the jacks. Below are some after pictures. The amp works great with the RCA jacks and this is a welcome development for me. Once I was done the top went back on and it was placed back into service.

Finished wiring up the phase splitter. For the circuit, I used the ubiquitous long tail pair used in a Marshall Plexi 50 watt. Due to my use of larger coupling caps, it was very fussy to wire up, and I worried about some error causing all sorts of problems or emitting the magic smoke. Imagine my pleasure when I hooked it up to the function generator and captured the voltage it was placing on the grids of the EL34s.

We see the 3.12 volt sine wave coming in and the resulting 64.8/67.2 volts on the EL34 grids, a voltage gain of 21 or 26.5 db. I note the two outputs are very close in voltage.

Phase Splitter with the power tubes

Its days like this that a four channel scope with screen capture is a wonderful thing. We see the power stage operating properly when driven by the phase splitter. The EL34s are not well matched, as evidenced by their different idle currents, but this is good enough for a general smoke test…

Input Stage Checkout

Doing a smoke test on the input triodes. The input signal is a 3 volt square wave–I wanted to see what kind of voltages it could emit and these are delightfully high. The configuration here is the typical Marshall input with a regular and ‘high’ stage. The difference being in the bias resistor and capacitor. The different responses to the square wave are to be expected. Here we are seeing a voltage gain of 18.7 on one and 23 on the other, or 16 and 17.6 db. Since the phase splitter is emitting close to full power driving voltage with a 3 volt input, I will need to look at how I want to structure the gain staging in the amp. I will not have a traditional tone control circuit, so the means of hooking it up to the phase splitter input will require some experimentation. There will be a rheostat for each side of the triode pair, and the relative levels there act to some extent as a tone control. A single input will drive the triodes, acting as the traditional jumper between the regular and high inputs.

After some years of low external interest and inaction on my part, my wordpress was hacked and from what I can determine, its content was lost. I didn’t see the need to try and recover old posts, and felt it was as good a time as any to make a fresh start. I am thinking this is where I can put professional technology posts that can be linked to in linkedin and facebook.

Mark Knutson WordPress site, rebuilding after hack